Direct convolution

Re-posted from: https://pixorblog.wordpress.com/2016/07/17/direct-convolution/

For small kernels, direct convolution beats FFT based one. I present here a basic implementation. This implementation allows to compute

$\gamma[k]=\sum\limits_{i\in\Omega^\alpha}\alpha[i]\beta[k+\lambda i],\text{ with }\lambda\in\mathbb{Z}^*\text{\ \ \ \ \ \ \ \ \ \ \ \ (1)}$

From time to time we will use the notation $\gamma=\alpha\bigodot\limits_\lambda\beta$ .

An arbitrary stride $\lambda$ has been introduced to define:

$\lambda=-1$ convolution
$\lambda=+1$ cross-correlation
$\lambda=\pm 2^n$ the stationary wavelet transform (the so called “à trous” algorithm)

Also note that with proper boundary extension (periodic and zero padding essentially), changing the sign of $\lambda$ gives the adjoint operator:

$\langle \delta, \alpha\bigodot\limits_\lambda\beta \rangle = \langle \alpha\bigodot\limits_{-\lambda}\delta,\beta \rangle$

Disclaimer

Maybe the following is overwhelmingly detailed for a simple task like Eq. (1), but I have found some interests in writing this once for all. Maybe it can be useful for someone else.

Some notations

We note $\Omega$ our vector domain (or support), for instance

$\Omega^\alpha =\llbracket i_{\min} ,i_{\max} \rrbracket$

means that $\alpha[i]$ is defined for

$i\in \llbracket i_{\min}, i_{\max} \rrbracket$

To get interval lower/upper bounds we use the notation

$i_{\min}=l(\Omega^\alpha)\text{ and }i_{\max}=u(\Omega^\alpha)$

We denote by $\lambda\Omega$ the scaled domain $\Omega$ defined by:

$\lambda\Omega=\llbracket \lambda^+\,i_{min}+\lambda^-\,i_{max}, \lambda^+\,i_{max}+\lambda^-\,i_{min} \rrbracket$

where $\lambda^+=\max{(0,\lambda)}$ and $\lambda^-=\min{(0,\lambda)}$

Finally we use $A\setminus B$ the relative complement of $B$ with respect to the set $A$ defined by

$A\setminus B = \{ i\ /\ (i\in A) \wedge (i\notin B) \}$

This set is not necessary connex, however like we are working in $\mathbb{Z}$ , it is sufficient to introduce the left and right parts (that can be empty)

$(A\setminus B)_{\text{Left}}=\llbracket l(A), \min{(u(A),l(B)-1)} \rrbracket$

$(A\setminus B)_{\text{Right}}=\llbracket \max{(l(A),u(B)+1)}, u(A) \rrbracket$

Goal

Given two vectors $\alpha$ , $\beta$ defined on $\Omega^\alpha$ , $\Omega^\beta$ we want to define and implement an algorithm that computes $\gamma[k]$ for $k\in\Omega^\gamma$ .

First step, no boundary extension

We need to define the $\Omega^\gamma_1$ the domain that does not violate $\beta$ domain of definition. This can be expressed as

$\Omega^\gamma_1=\{k\in\mathbb{Z}\ /\ \forall i \in \Omega^\alpha \Rightarrow k+\lambda i \in \Omega^\beta \}$

Let’s write the details,

$(\forall i \in \Omega^\alpha \Rightarrow k+\lambda i \in \Omega^\beta)\Leftrightarrow (\forall i \in \Omega^\alpha \Rightarrow l(\Omega^\beta)-\lambda i \le k \le u(\Omega^\beta)-\lambda i)$

$\Leftrightarrow \max\limits_{i\in \Omega^\alpha} l(\Omega^\beta)-\lambda i \le k \le \min\limits_{i\in \Omega^\alpha} u(\Omega^\beta)-\lambda i$

$\Leftrightarrow l(\Omega^\beta)-l(\lambda \Omega^\alpha) \le k \le u(\Omega^\beta)-u(\lambda \Omega^\alpha)$

hence we have

$\boxed{ \Omega^\gamma_1=\llbracket l(\Omega^\beta)-l(\lambda \Omega^\alpha) , u(\Omega^\beta)-u(\lambda \Omega^\alpha) \rrbracket }$

Thus the computation of $\gamma[k],\ k\in\Omega^\gamma$ (Eq. 1) is splitted into two parts:

one part $\Omega^\gamma \cap \Omega^\gamma_1$ free of boundary effect,
one part $\Omega^\gamma \setminus \Omega^\gamma_1$ that requires boundary extension $\tilde{\beta}=\Phi(\beta,k)$

The algorithm takes the following form:

$latex-test.png$

Second step, boundary extensions

Usually we define some classical boundary extensions. These extensions are computed from $\beta[.]$ and are sometimes entailed by a validity condition. For a better clarity I give explicit lower/upper bounds:

$\Omega^\beta = \llbracket j_{\min} , j_{\max} \rrbracket \neq \emptyset$

Left boundary $(j<j_{min})$	$\tilde{\beta}_j = \Phi_{left}(\beta,j)$	validity condition
Mirror	$\tilde{\beta}_j = \beta[2\,j_{min}-j]$	$2\,j_{min}-j_{max} \le j$
Periodic (or cyclic)	$\tilde{\beta}_j = \beta[j_{max}-j_{min}+j+1]$	$2\,j_{min}-j_{max}-1 \le j$
Constant	$\tilde{\beta}_j = \beta[j_{min}]$	none
Zero padding	$\tilde{\beta}_j = 0$	none

Right boundary $(j>j_{max})$	$\tilde{\beta}_j = \Phi_{right}(\beta,j)$	validity condition
Mirror	$\tilde{\beta}_j = \beta[2\,j_{max}-j]$	$j\le 2\,j_{max}-j_{min}$
Periodic (or cyclic)	$\tilde{\beta}_j = \beta[-j_{max}+j_{min}+j-1]$	$j\le 2\,j_{max}-j_{min}+1$
Constant	$\tilde{\beta}_j = \beta[j_{max}]$	none
Zero padding	$\tilde{\beta}_j = 0$	none

As we want something general we want to get rid of these validity conditions.

Periodic case

Starting from a vector $\beta$ defined on $\llbracket L=0, U \rrbracket$ we want to define a periodic function $\tilde{\beta}$ of period $T=U+1$ . This function must fulfills the $\tilde{\beta}[j+T]=\tilde{\beta}[j]$ relation.

We can do that by considering $\tilde{\beta}=\beta \circ \phi^P_U(j)$ where

$\phi^P_U(j)=\bmod_F(j,U+1)$

and $\bmod_F$ is the modulus function associated to a floored division.

For a vector defined on an arbitrary domain $\llbracket j_{\min}, j_{\max} \rrbracket$ , we first translate the indices

$\tau_{j_{\min}}(j)=j-j_{\min}$

and then translate them back using $\tau^{(-1)}_{j_{\min}}=\tau_{-j_{\min}}$

Putting all together, we build a periodized vector

$\boxed{\tilde{\beta} = \beta \circ \phi^P_{j_{\min},j_{\max}}}$

where

$\phi^P_{j_{\min},j_{\max}} = \tau^{(-1)}_{j_{\min}} \circ \phi^P_{j_{\max}- j_{\min}} \circ \tau_{j_{\min}}$

$\boxed{\phi^P_{j_{\min},j_{\max}} = j_{\min} + \bmod_F(j-j_{\min},j_{\max}- j_{\min}+1)}$

Mirror Symmetry case

Starting from a vector $\beta$ defined on $\llbracket L=0, U \rrbracket$ we can extend it by mirror symmetry on $\llbracket U+1, 2U \rrbracket$ using $\tilde{\beta}=\beta\circ \phi^M_U$ with

$\phi^M_U(j)=U-|U-j|$

The resulting vector $\tilde{\beta}=\beta\circ \phi^M_U$ fulfills the $\tilde{\beta}[U-j]=\tilde{\beta}[U+j]$ relation for $j\in \llbracket 0, U \rrbracket$ .

To get a “global” definition we then periodize it on $\llbracket 0, 2U-1 \rrbracket$ using $\phi^P_{2U-1}$ (attention $2U-1$ and not $2U$ , otherwise the component $0$ is duplicated!).

For an arbitrary domain $\llbracket j_{\min}, j_{\max} \rrbracket$ we use index translation as for the periodic case. Putting everything together we get:

$\boxed{\tilde{\beta} = \beta \circ \phi^M_{j_{\min},j_{\max}}}$

where

$\phi^M_{j_{\min},j_{\max}} = \tau^{(-1)}_{j_{\min}} \circ \phi^M_{j_{\max}- j_{\min}} \circ \phi^P_{2(j_{\max}- j_{\min})-1} \circ \tau_{j_{\min}}$

$\boxed{ \phi^M_{j_{\min},j_{\max}} =j_{\max}-|j_{\max}-j_{\min}-\bmod_F(j-j_{\min},2(j_{\max}-j_{\min}))| }$

Boundary extensions

To use the algorithm with boundary extensions, you only have to define:

$\tilde{\beta}=\Phi(\beta,k+\lambda i)=\beta[\phi^X[k+\lambda i]]$

where $X$ is the boundary extension you have chosen (periodic, constant). You do not have to take care of any validity condition, these formula are general.

Implementation

This is a straightforward implementation following as close as possible the presented formula. We did not try to optimize it, this would have obscured the presentation. Some ideas: reverse $\alpha$ for $\lambda<0$ (access memory in the right order), use simd, or C++ meta-programming with loop unrolling for fixed $\alpha$ size, specialize regarding to Vector/StridedVector or $\lambda=\pm 1$

Preamble

Index translation / domain definition

There is however one last thing we have to explain. In languages like Julia, C we are manipulating arrays having a common starting index: $1$ in Julia, Fortran or $0$ in C, C++

For this reason we do not manipulate $\alpha$ on $\Omega^\alpha$ but an another translated array $\tilde{\alpha}$ defined on $\llbracket 1, N^\alpha \rrbracket$ (Julia) or $\llbracket 0, N^\alpha-1 \rrbracket$ (C++).

To cover all cases, I assume that the starting index is denoted by $\tilde{i}_0$ .

The array $\tilde{\alpha}$ is defined by:

$\alpha[i] = \tilde{\alpha}[\tilde{i}] = \tilde{\alpha}[i-l(\Omega^\alpha)+\tilde{i}_0]$

Hence we must modify the initiale Eq. (1) to use $\tilde{\alpha}$ instead of $\alpha$

$\gamma[k]=\sum\limits_{i\in\Omega^\alpha}\alpha[i]\beta[k+\lambda i] = \sum\limits_{i\in\Omega^\alpha}\tilde{\alpha}[i-l(\Omega^\alpha)+\tilde{i}_0]\beta[k+\lambda i]$

With $\tilde{i}=i-l(\Omega^\alpha)+\tilde{i}_0$ we have

$i\in\Omega^\alpha \Leftrightarrow \tilde{i}\in\llbracket \tilde{i}_0,u(\Omega^\alpha)-l(\Omega^\alpha)+\tilde{i}_0 \rrbracket$

and

$k+\lambda i = k+ \lambda \tilde{i} + \underbrace{\lambda (l(\Omega^\alpha) - \tilde{i}_0)}_{\beta\_\text{offset}}$

Thus, Eq (1) becomes:

$\boxed{ \gamma[k]=\sum\limits_{\tilde{i}=\tilde{i}_0}^{u(\Omega^\alpha)-l(\Omega^\alpha)+\tilde{i}_0}\tilde{\alpha}[\tilde{i}]\beta[k+ \lambda \tilde{i} + \lambda (l(\Omega^\alpha) - \tilde{i}_0)]}$

The $2$ other arrays are less problematic:

For $\beta$ array, which is our input array, we implicitly use $\Omega^\beta = \llbracket \tilde{i}_0, \tilde{i}_0 + \text{length}(\beta) - 1 \rrbracket$ . This does not reduce the generality of the subroutine.
For $\gamma$ which is the output array, as for $\beta$ we assume it is defined on $\llbracket \tilde{i}_0, \tilde{i}_0 + \text{length}(\gamma) - 1 \rrbracket$ , but we provide $\Omega^\gamma\subset \llbracket \tilde{i}_0, \tilde{i}_0 + \text{length}(\gamma) - 1 \rrbracket$ to define the components we want to compute. The other components, $\llbracket \tilde{i}_0, \tilde{i}_0 + \text{length}(\gamma) - 1 \rrbracket \setminus \Omega^\gamma$ , will remain unmodified by the subroutine.

Definition of 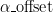$\alpha\_\text{offset}$

As we have seen before, the convolution subroutine will have $\tilde{\alpha}$ as argument, but we also need $\Omega^\alpha$ . For the driver subroutine we do not directly provide this interval because its length is redundant with $\tilde{\alpha}$ length. Instead we provide an $\alpha\_\text{offset}$ offset. $\Omega^\alpha$ is deduced from:

$\Omega^\alpha = \llbracket -\alpha\_\text{offset}, -\alpha\_\text{offset} + \text{length}(\tilde{\alpha}) -1 \rrbracket$

Note: this definition does not depend on $\tilde{i}_0$ .

With $\alpha\_\text{offset}=0$ you are in the “usual situation”. If you have a window size of $2n+1$ , taking $\alpha\_\text{offset}=n$ returns the middle of the window. Here, in the Fig. below, the graphical representation of an arbitrary case: a filter if size $4$ , with $\alpha\_\text{offset}=2$ and $\lambda=3$ .

Julia

Auxiliary subroutines

We start by defining the basic operations on sets:

function scale(λ::Int64,Ω::UnitRange)
    ifelse(λ>0,
           UnitRange(λ*start(Ω),λ*last(Ω)),
           UnitRange(λ*last(Ω),λ*start(Ω)))
end

function compute_Ωγ1(Ωα::UnitRange,
                     λ::Int64,
                     Ωβ::UnitRange)
    
    λΩα = scale(λ,Ωα)

    UnitRange(start(Ωβ)-start(λΩα),
              last(Ωβ)-last(λΩα))
end

# Left & Right relative complements A\B
#
function relelativeComplement_left(A::UnitRange,
                                   B::UnitRange)
    UnitRange(start(A),
              min(last(A),start(B)-1))
end

function relelativeComplement_right(A::UnitRange,
                                    B::UnitRange)
    UnitRange(max(start(A),last(B)+1),
              last(A))
end

Boundary extensions

We then define the boundary extensions. Nothing special there, we only had to check that the Julia mod(x,y) function is the floored division version (by opposition to the rem(x,y) function which is the rounded toward zero division version).

const tilde_i0 = Int64(1)

function boundaryExtension_zeroPadding{T}(β::StridedVector{T},
                                          k::Int64)
    kmin = tilde_i0
    kmax = length(β) + kmin - 1
    
    if (k>=kmin)&&(k<=kmax)
        β[k]
    else
        T(0)
    end
end

function boundaryExtension_constant{T}(β::StridedVector{T},
                                       k::Int64)
    kmin = tilde_i0
    kmax = length(β) + kmin - 1

    if k<kmin
        β[kmin]
    elseif k<=kmax
        β[k]
    else
        β[kmax]
    end
end

function boundaryExtension_periodic{T}(β::StridedVector{T},
                                       k::Int64)
    kmin = tilde_i0
    kmax = length(β) + kmin - 1

    β[kmin+mod(k-kmin,1+kmax-kmin)]
end

function boundaryExtension_mirror{T}(β::StridedVector{T},
                                     k::Int64)
    kmin = tilde_i0
    kmax = length(β) + kmin - 1

    β[kmax-abs(kmax-kmin-mod(k-kmin,2*(kmax-kmin)))]
end

# For the user interface
#
boundaryExtension = 
    Dict(:ZeroPadding=>boundaryExtension_zeroPadding,
         :Constant=>boundaryExtension_constant,
         :Periodic=>boundaryExtension_periodic,
         :Mirror=>boundaryExtension_mirror)

Main subroutine

Finally we define the main subroutine. Its arguments have been defined in the preamble part. I just added one @simd & @inbounds because this has a significant impact concerning perfomance (see end of this post).

function direct_conv!{T}(tilde_α::StridedVector{T},
                         Ωα::UnitRange,
                         λ::Int64,
                         β::StridedVector{T},
                         γ::StridedVector{T},
                         Ωγ::UnitRange,
                         LeftBoundary::Symbol,
                         RightBoundary::Symbol)
    # Sanity check
    @assert λ!=0
    @assert length(tilde_α)==length(Ωα)
    @assert (start(Ωγ)>=1)&&(last(Ωγ)<=length(γ))

    # Initialization
    Ωβ = UnitRange(1,length(β))
    tilde_Ωα = 1:length(Ωα)
    
    for k in Ωγ
        γ[k]=0 
    end

    rΩγ1=intersect(Ωγ,compute_Ωγ1(Ωα,λ,Ωβ))
    
    # rΩγ1 part: no boundary effect
    #
    β_offset = λ*(start(Ωα)-tilde_i0)
    @simd for k in rΩγ1
        for i in tilde_Ωα
            @inbounds γ[k]+=tilde_α[i]*β[k+λ*i+β_offset]
        end
    end

    # Left part
    #
    rΩγ1_left = relelativeComplement_left(Ωγ,rΩγ1)
    Φ_left = boundaryExtension[LeftBoundary]
    
    for k in rΩγ1_left
        for i in tilde_Ωα
            γ[k]+=tilde_α[i]*Φ_left(β,k+λ*i+β_offset)
        end
    end

    # Right part
    #
    rΩγ1_right = relelativeComplement_right(Ωγ,rΩγ1)
    Φ_right = boundaryExtension[RightBoundary]
    
    for k in rΩγ1_right
        for i in tilde_Ωα
            γ[k]+=tilde_α[i]*Φ_right(β,k+λ*i+β_offset)
        end
    end
end

# Some UI functions, γ inplace modification 
#
function direct_conv!{T}(tilde_α::StridedVector{T},
                         α_offset::Int64,
                         λ::Int64,

                         β::StridedVector{T},

                         γ::StridedVector{T},
                         Ωγ::UnitRange,
                         
                         LeftBoundary::Symbol,
                         RightBoundary::Symbol)

    Ωα = UnitRange(-α_offset,
                   length(tilde_α)-α_offset-1)
    
    direct_conv!(tilde_α,
                 Ωα,
                 λ,
                 
                 β,

                 γ,
                 Ωγ,

                 LeftBoundary,
                 RightBoundary)
end

# Some UI functions, allocates γ 
#
function direct_conv{T}(tilde_α::StridedVector{T},
                        α_offset::Int64,
                        λ::Int64,

                        β::StridedVector{T},

                        LeftBoundary::Symbol,
                        RightBoundary::Symbol)

    γ = Array{T,1}(length(β))
    
    direct_conv!(tilde_α,
                 α_offset,
                 λ,

                 β,

                 γ,
                 UnitRange(1,length(γ)),

                 LeftBoundary,
                 RightBoundary)

    γ
end

In C/C++

As this post is already long I will not provide a complete code here. The only trap is to use the right mod function.

C/C++ modulus operator % is not standardized. Only the D%d=D-d*(D/d) relation is invariant allowing to define the Euclidean division. On the other side a lot of CPU x86 idiv, truncate toward zero, as a consequence C/C++ generally uses this direction.

To be sure, we have to explicitly use our F-mod function:

// Floored mod
int modF(int D, int d)
{
    int r = std::fmod(D,d);
    if((r > 0 && d < 0) || (r < 0 && d > 0)) r = r + d;
    return r;
}

You can read:

Usages examples

Basic usages

Beware that due to the asymmetric role of $\alpha$ and $\beta$ the proposed approach does preserve all the mathematical properties of the $\alpha\bigodot\limits_\lambda\beta$ operator.

Commutativity:

$\alpha\bigodot\limits_{\lambda=-1}\beta=\beta\bigodot\limits_{\lambda=-1}\alpha$

only for ZeroPadding

Adjoint operator:

$\forall \lambda\in\mathbb{Z}^*,\ \langle \alpha\bigodot\limits_{\lambda}v ,w \rangle_E = \langle v , \alpha\bigodot\limits_{-\lambda} w \rangle_F$

only for ZeroPadding and Periodic

I have assumed $\mathbb{R}$ arrays (not $\mathbb{C}$ ones): some conjugation are missing
Not considered here, but extension to n-dimensional & separable filters is immediate

push!(LOAD_PATH,"./")
using DirectConv

α=rand(4);
β=rand(10);

# Check adjoint operator
# -> restricted to ZeroPadding & Periodic
#    (asymmetric role of α and β)
#    
vβ=rand(length(β))
d1=dot(direct_conv(α,2,-3,vβ,:ZeroPadding,:ZeroPadding),β)
d2=dot(direct_conv(α,2,+3,β,:ZeroPadding,:ZeroPadding),vβ)

@assert abs(d1-d2)<sqrt(eps())

d1=dot(direct_conv(α,-1,-3,vβ,:Periodic,:Periodic),β)
d2=dot(direct_conv(α,-1,+3,β,:Periodic,:Periodic),vβ)

@assert abs(d1-d2)<sqrt(eps())

# Check commutativity 
# -> λ = -1 (convolution) and
#    restricted to ZeroPadding
#    (asymmetric role of α and β)
v1=zeros(20)
v2=zeros(20)
direct_conv!(α,0,-1,
             β,v1,UnitRange(1,20),:ZeroPadding,:ZeroPadding)
direct_conv!(β,0,-1,
             α,v2,UnitRange(1,20),:ZeroPadding,:ZeroPadding)

@assert (norm(v1-v2)<sqrt(eps()))

# Check Interval splitting
# (should work for any boundary extension type)
#
γ=direct_conv(α,3,2,β,:Mirror,:Periodic) # global computation
Γ=zeros(length(γ))
Ω1=UnitRange(1:3)
Ω2=UnitRange(4:length(γ))
direct_conv!(α,3,2,β,Γ,Ω1,:Mirror,:Periodic) # compute on Ω1
direct_conv!(α,3,2,β,Γ,Ω2,:Mirror,:Periodic) # compute on Ω2

@assert (norm(γ-Γ)<sqrt(eps()))

Performance?

In a previous post I gave a short derivation of the Savitzky-Golay filters. I used a FFT based convolution to apply the filters. It is interesting to compare the performance of the presented direct approach vs the FFT one.

push!(LOAD_PATH,"./")
using DirectConv

function apply_filter{T}(filter::StridedVector{T},signal::StridedVector{T})

    @assert isodd(length(filter))

    halfWindow = round(Int,(length(filter)-1)/2)
    
    padded_signal = 
        [signal[1]*ones(halfWindow);
         signal;
         signal[end]*ones(halfWindow)]

    filter_cross_signal = conv(filter[end:-1:1],
                               padded_signal)

    filter_cross_signal[2*halfWindow+1:end-2*halfWindow]
end

# Now we can create a (very) rough benchmark
M=Array(Float64,0,3)
β=rand(1000000);
for halfWidth in 1:2:40
    α=rand(2*halfWidth+1);

    fft_t0 = time()
    fft_v = apply_filter(α,β)
    fft_t1 = time()

    direct_t0 = time()
    direct_v = direct_conv(α,halfWidth,1,β,
                           :Constant,:Constant)
    direct_t1 = time()

    @assert (norm(fft_v -direct_v)<sqrt(eps()))

    M=vcat(M,
           Float64[length(α)
                   (fft_t1-fft_t0)*1e3
                   (direct_t1-direct_t0)*1e3])
end
M

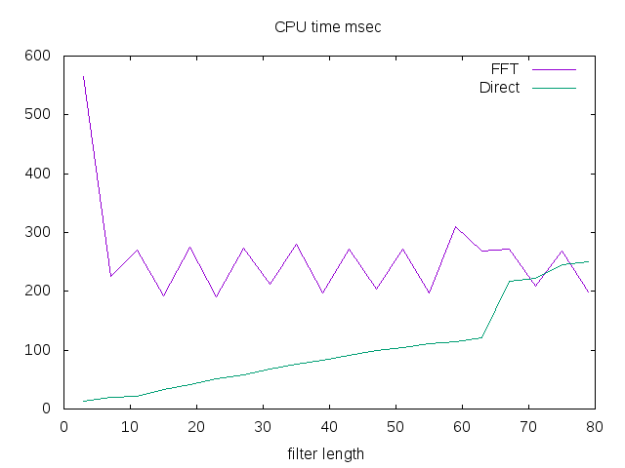
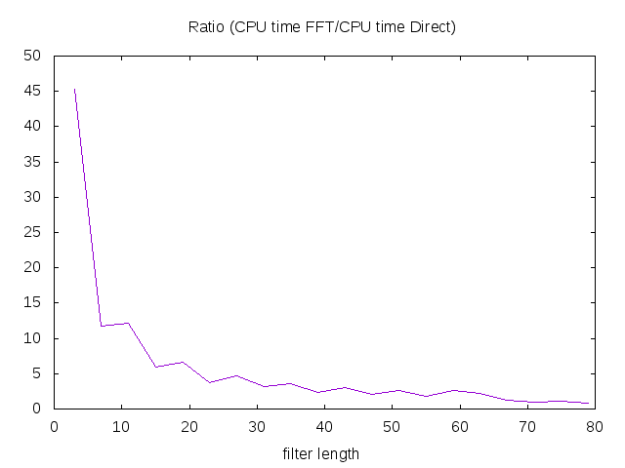
We see that for small filters direct method can easily be 10 time faster than the FFT approach!

Conclusion: for small filters, use a direct approach!

Discussion

Optimization/performance

If I have time I will try to benchmark two basic implementations, a Julia one vs a C/C++ one. I’m a beginner in Julia language, with C++, I’m more at home.

I would be curious to see the difference between a basic implementation and an optimized one in Julia. Just to see how optimization can obfuscate (or not) the initial code and the performance gain. In C++ you generally have a lot of boiler-plate code (meta-programming).

Applications

The basic Eq. (1) is common tool that can be used for:

deconvolution procedures,
decimated and undecimated wavelet transforms,

For wavelet transform especially the undecimated one, AFAIK Eq. (1) is really the good choice. I will certainly write some posts on these stuff.

Some extra reading:

The FFT way: Algorithms for Efficient Computation of Convolution, K. Pavel
The Winograd’s minimal filtering algorithms way: Fast Algorithms for Convolutional Neural Networks, A. Lavin, S. Gray
The OpenCL/GUPU way: Case study: High performance convolution using OpenCL __local memory

Code

The code is on github.

Complement: more domains

The 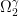$\Omega^\gamma_2$ domain

We have introduced $\Omega^\gamma_1$ the domain that does not violate $\beta$ domain of definition (given $\Omega^\alpha$ and $\Omega^\beta$ ).

To be exhaustive we can introduce $\Omega^\gamma_2$ the domain that use at least one $(i,k+\lambda i)\in \Omega^\alpha \times \Omega^\beta$ .

This domain is:

$\Omega^\gamma_2=\{ k\in\mathbb{Z}\ /\ \exists i \in \Omega^\alpha \Rightarrow k+\lambda i \in \Omega^\beta \}$

following arguments similar to those used for $\Omega^\gamma_1$ we get:

$\boxed{ \Omega^\gamma_2=\llbracket l(\Omega^\beta)-u(\lambda \Omega^\alpha) , u(\Omega^\beta)-l(\lambda \Omega^\alpha) \rrbracket }$

The $\Omega^\beta_{2'}$ domain

We can also ask for the “dual” question: given $\Omega^\alpha$ and $\Omega^\gamma$ what is the domain of $\beta$ , $\Omega^\beta_{2'}$ , involved in the computation of $\gamma$

By definition, this domain must fulfill the following relation:

$\Omega^\gamma_2(\Omega^\beta_{2'})=\Omega^\gamma$

hence, using the previous result

$\llbracket l(\Omega^\beta_{2'})-u(\lambda \Omega^\alpha) , u(\Omega^\beta_{2'})-l(\lambda \Omega^\alpha) \rrbracket = \llbracket l(\Omega^\gamma),u(\Omega^\gamma) \rrbracket$

which gives:

$\boxed{ \Omega^\beta_{2'} = \llbracket l(\Omega^\gamma)+u(\lambda \Omega^\alpha),u(\Omega^\gamma)+l(\lambda \Omega^\alpha) \rrbracket }$

juliabloggers.com

A Julia Language Blog Aggregator

Disclaimer

Some notations

Goal

First step, no boundary extension

Second step, boundary extensions

Periodic case

Mirror Symmetry case

Boundary extensions

Implementation

Preamble

Index translation / domain definition

Definition of $\alpha\_\text{offset}$

Julia

Auxiliary subroutines

Boundary extensions

Main subroutine

In C/C++

Usages examples

Basic usages

Performance?

Discussion

Optimization/performance

Applications

Code

Complement: more domains

The $\Omega^\gamma_2$ domain

The $\Omega^\beta_{2'}$ domain

Related

Disclaimer

Some notations

Goal

First step, no boundary extension

Second step, boundary extensions

Periodic case

Mirror Symmetry case

Boundary extensions

Implementation

Preamble

Index translation / domain definition

Definition of

Julia

Auxiliary subroutines

Boundary extensions

Main subroutine

In C/C++

Usages examples

Basic usages

Performance?

Discussion

Optimization/performance

Applications

Code

Complement: more domains

The domain

The domain

Related

Definition of $\alpha\_\text{offset}$

The $\Omega^\gamma_2$ domain

The $\Omega^\beta_{2'}$ domain