By: Picaud Vincent
Re-posted from: https://pixorblog.wordpress.com/2016/07/13/savitzky-golay-filters-julia/
I always have found that presentations of the Savitzky-Golay filters were over tricky. I present here a simple derivation of these formula and a possible implementation in Julia.
Derivation of the formula
Given a polynomial of degree with values
defined for a window of size ,
We want to find the value of its k-order derivative in the middle of the window assuming that the
are founded solving a least-squares problem:
where is our signal values and
is the Vandermonde matrix:
using the normal equation
and a QR decomposition, we get
now we can express all the polynomial values in a vector
. Lets rewrite this in matrix form:
Now the “big trick” is to write the Taylor series and to remember that this formula is exact for polynomial functions:
Lets rewrite this in matrix form:
With a good eye we see that where
is a diagonal matrix:
That’s all, we only have to group pieces:
With the QR decomposition and
we get:
using the fact that we get:
hence we have:
which is our final formula.
Symbolic computation to check that it works
We can use mathematica to do a symbolic computation using .
For a window width of points and a polynomial of degree
we get:
n = 3; d = 2;
V = Table[If[j != 0, i^j, 1], {i, -n, n}, {j, 0, d}];
{Qt, R} = QRDecomposition[V];
DD = DiagonalMatrix[Table[Factorial[i], {i, 0, d}]];
DD.Inverse[R].Qt // TeXForm
The first row is the smoothing filter, the second one the smoothed first order derivative
filter and the last one the smoothed second order derivative
filter.
A Julia implementation
Here I present a direct implementation in julia.
We first initialize a Vandermonde matrix:
function vandermonde(halfWindow::Int, polyDeg::Int,T::Type=Float64) @assert halfWindow>=0 @assert polyDeg>=0 x=T[i for i in -halfWindow:halfWindow] n = polyDeg+1 m = length(x) V = Array{T}(m, n) for i = 1:m V[i,1] = T(1) end for j = 2:n for i = 1:m V[i,j] = x[i] * V[i,j-1] end end return V end
We then compute the filter coefficients with the presented formula.
Attention we return the transposed matrix because in Julia it is more convenient to use SG[:,1] which is a julia vector. SG[1,:] would be a (1,n) julia matrix.
function SG(halfWindow::Int, polyDeg::Int,T::Type=Float64) @assert 2*halfWindow>polyDeg V=vandermonde(halfWindow,polyDeg,T) Q,R=qr(V) SG=R\Q' for i in 1:size(SG,1) SG[i,:]*=factorial(i-1) end # CAVEAT: returns the transposed matrix return SG' end
The final step to use the filter is to provide function to do the cross-correlation.
I do not want to talk too much about this subroutine because in a future post I will show how to efficiently compute such kind of convolution. Here we use a FFT, but with a short filter it is much more efficient (around 10 times faster) to use a direct computation. I will show how to implement
which can be used to compute discrete and stationary wavelet transform for instance.
One last thing, here we use constant padding to manage the boundaries.
function apply_filter{T}(filter::StridedVector{T},signal::StridedVector{T}) @assert isodd(length(filter)) halfWindow = round(Int,(length(filter)-1)/2) padded_signal = [signal[1]*ones(halfWindow); signal; signal[end]*ones(halfWindow)] filter_cross_signal = conv(filter[end:-1:1], padded_signal) return filter_cross_signal[2*halfWindow+1:end-2*halfWindow] end
Finally I have included a small usage example. To see well the effect of Savitzky-Golay filters, I have over smoothed with a large window width ,
using Winston s=readdlm("signal.txt")[:,1] sg=SG(20,3) # halt-window, polynomal degree #________________ smoothed=apply_filter(sg[:,1],s) plot(s,"r") oplot(smoothed) title("Smoothed") savefig("smoothed.png") #________________ smoothed_d1=apply_filter(sg[:,2],s) plot(smoothed_d1) title("Smoothed derivative") savefig("smoothed_d1.png") #________________ smoothed_d2=apply_filter(sg[:,3],s) plot(smoothed_d2) title("Smoothed 2-derivative") savefig("smoothed_d2.png")
Here is the resulting plots:
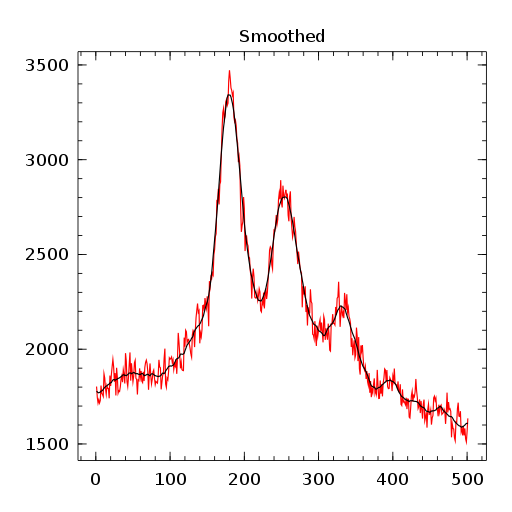
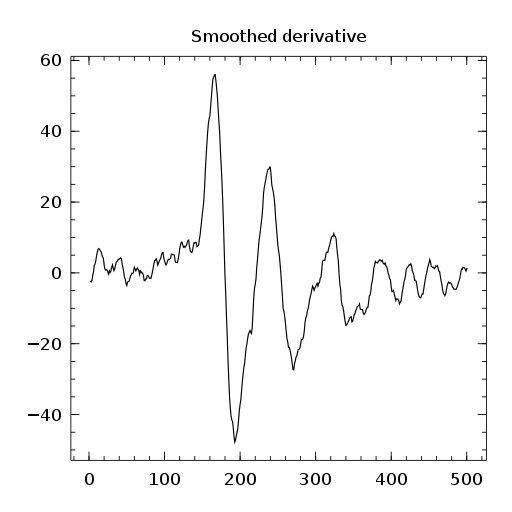
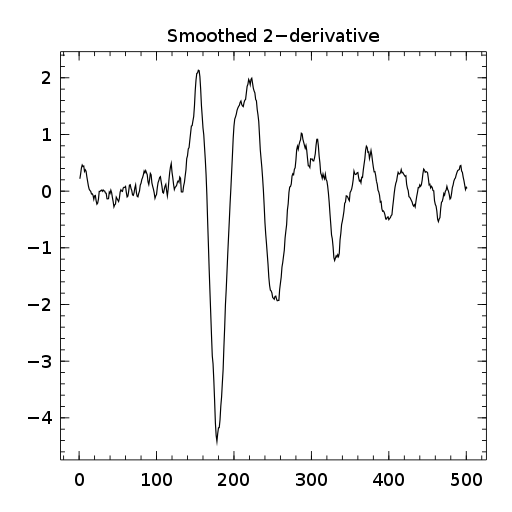
Final word
To reproduce these figures you can find the complete code on github.