Tag Archives: econometrics

An Introduction to Structural Econometrics in Julia

Re-posted from: http://juliaeconomics.com/2016/02/09/an-introduction-to-structural-econometrics-in-julia/

This tutorial is adapted from my Julia introductory lecture taught in the graduate course Practical Computing for Economists, Department of Economics, University of Chicago.

The tutorial is in 5 parts:

Installing Julia + Juno IDE, as well as useful packages
Defining a structural econometric challenge
Data generation, management, and regression visualization
Numerical simulation of optimal agent behavior under constraints
Parallelized estimation by the Method of Simulated Moments

1. Installing Julia + Juno IDE, as well as useful packages

Perhaps the greatest obstacle to using Julia in the past has been the absence of an easy-to-install IDE. There used to be an IDE called Julia Studio which was as easy to use as the popular RStudio for R. Back then, you could install and run Julia + Julia Studio in 5mins, compared to the hours it could take to install Python and its basic packages and IDE. When Julia version 0.3.X was released, Julia Studio no longer worked, and I recommended the IJulia Notebook, which requires the installation of Python and IPython just to use Julia, so any argument that Julia is more convenient to install than Python was lost.

Now, with Julia version 0.4.X, Juno has provided an excellent IDE that comes pre-bundled with Julia for convenience, and you can install Julia + Juno IDE in 5mins. Here are some instructions to help you through the installation process:

Go to http://julialang.org/downloads/ and look for “Julia + Juno IDE bundles“. Click to download the bundle for your system (Windows, Mac, or Linux).
After the brief download (the entire Julia language + Juno IDE is less than 1GB), open the file and click through the installation instructions.
Open Juno, and try to run a very simple line of code. For example, type 2+2, highlight this text, right-click, and choose the option Evaluate. A bubble should display 4 next to the line of code.
- Trouble-shooting: On my Mac running OS X Mavericks, 2+2 failed and an unhelpful error was produced. After some searching, I found that the solution was to install the Jewel package. To install Jewel from within Juno, just type Pkg.add(“Jewel”), highlight this text, and Evaluate. After this, 2+2 was successful.
You have successfully installed Julia + Juno IDE, which includes a number of important packages already, such as DataFrames, Gadfly, and Optim. Now, you will want to run the following codes to install some other packages used in the econometric exercises below:

Pkg.update()
Pkg.add("Ipopt")
Pkg.build("Ipopt")
Pkg.add("JuMP")
Pkg.build("JuMP")
Pkg.add("GLM")
Pkg.add("KernelEstimator")

2. Defining a structural econometric challenge

To motivate our application, we consider a very simple economic model, which I have taught previously in the mathematical economics course for undergraduates at the University of Chicago. Although the model is analytically simple, the econometrics become sufficiently complicated to warrant the Method of Simulated Moments, so this serves us well as a teachable case.

Let $c_i \geq 0$ denote consumption and $0 \leq l_i \leq 1$ denote leisure. Consider an agent who wishes to maximize Cobb-Douglas utility over consumption and leisure, that is,

$U(c_i,l_i) =$ $c^\gamma_i l^{1-\gamma}_i$ .

where $0 \leq \gamma \leq 1$ is the relative preference for consumption. The budget constraint is given by,

$c_i \leq (1-\tau)w_i(1-l_i)+\epsilon_i$ ,

where $w_i$ is the wage observed in the data, $\epsilon_i$ is other income that is not observed in the data, and $\tau$ is the tax rate.

The agent’s problem is to maximize $U(c_i,l_i)$ subject to the budget constraint. We assume that non-labor income is uncorrelated with the wage offer, so that $\mathbb{E}[\epsilon_i | w_i]=0$ . Although this assumption is a bit unrealistic, as we expect high-wage agents to also tend to have higher non-labor income, it helps keep the example simple. The model is also a bit contrived in that we treat the tax rate as unobservable, but this only makes our job more difficult.

The goal of the econometrician is to identify the model parameters $\gamma$ and $\tau$ from the data $(c_i,l_i,w_i)^N_{i=1}$ and the assumed structure. In particular, the econometrician is interested in the policy-relevant parameter $\bar\psi \equiv \frac{1}{N}\sum^N_{i=1}\psi(w_i)$ , where,

$\psi(w_i) \equiv \mathbb{E}_{\epsilon} \frac{\partial}{\partial \tau} C(w_i,\epsilon; \gamma, \tau)$ ,

and $C(\cdot)$ denotes the demand for consumption. $\psi(w_i)$ is the marginal propensity for an agent with wage $w_i$ to consume in response to the tax rate. $\bar{\psi}$ is the population average marginal propensity to consume in response to the tax rate. Of course, we can solve the model analytically to find that $\psi(w_i) = -\gamma w_i$ and $\bar\psi = -\gamma \bar{w}$ , where $\bar{w}$ is the average wage, but we will show that the numerical methods achieve the correct answer even when we cannot solve the model.

3. Data generation, management, and regression visualization

The replication code for this section is available here.

To generate data that follows the above model, we first solve analytically for the demand functions for consumption and leisure. In particular, they are,

$C(w_i,\epsilon_i; \gamma, \tau) = \gamma (1-\tau) w_i + \gamma \epsilon_i$

$L(w_i,\epsilon_i; \gamma, \tau) = (1-\gamma) + \frac{(1-\gamma) \epsilon_i}{ (1-\tau) w_i}$

Thus, we need only draw values of $w_i$ and $\epsilon_i$ , as well as choose parameter values for $\gamma$ and $\tau$ , in order to generate the values of $c_i$ and $l_i$ that agents in this model would choose. We implement this in Julia as follows:

####### Set Simulation Parameters #########
srand(123)           # set the seed to ensure reproducibility
N = 1000             # set number of agents in economy
gamma = .5           # set Cobb-Douglas relative preference for consumption
tau = .2             # set tax rate

####### Draw Income Data and Optimal Consumption and Leisure #########
epsilon = randn(N)                                               # draw unobserved non-labor income
wage = 10+randn(N)                                               # draw observed wage
consump = gamma*(1-tau)*wage + gamma*epsilon                     # Cobb-Douglas demand for c
leisure = (1.0-gamma) + ((1.0-gamma)*epsilon)./((1.0-tau)*wage)  # Cobb-Douglas demand for l

This code is relatively self-explanatory. Our parameter choices are $N=1000$ , $\epsilon_i \sim \mathcal{N}(0,1)$ , $\gamma=1/2$ , and $\tau=1/5$ . We draw the wage to have distribution $w_i \sim \mathcal{N}(10,1)$ , but this is arbitrary.

We combine the variables into a DataFrame, and export the data as a CSV file. In order to better understand the data, we also non-parametrically regress $c_i$ on $w_i$ , and plot the result with Gadfly. The Julia code is as follows:

####### Organize, Describe, and Export Data #########
using DataFrames
using Gadfly
df = DataFrame(consump=consump,leisure=leisure,wage=wage,epsilon=epsilon)  # create data frame
plot_c = plot(df,x=:wage,y=:consump,Geom.smooth(method=:loess))            # plot E[consump|wage] using Gadfly
draw(SVG("plot_c.svg", 4inch, 4inch), plot_c)                              # export plot as SVG
writetable("consump_leisure.csv",df)                                       # export data as CSV

Again, the code is self-explanatory. The regression graph produced by the plot function is:

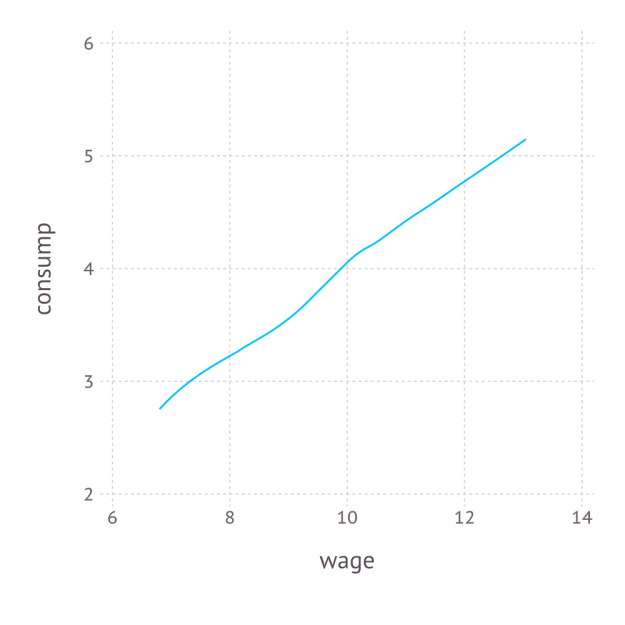
plot_c

4. Numerical simulation of optimal agent behavior under constraints

The replication code for this section is available here.

We now use constrained numerical optimization to generate optimal consumption and leisure data without analytically solving for the demand function. We begin by importing the data and the necessary packages:

####### Prepare for Numerical Optimization #########

using DataFrames
using JuMP
using Ipopt
df = readtable("consump_leisure.csv")
N = size(df)[1]

Using the JuMP syntax for non-linear modeling, first we define an empty model associated with the Ipopt solver, and then add $N$ values of $c_i$ and $N$ values of $l_i$ to the model:

m = Model(solver=IpoptSolver())    # define empty model solved by Ipopt algorithm
@defVar(m, c[i=1:N] >= 0)       # define positive consumption for each agent
@defVar(m, 0 <= l[i=1:N] <= 1)  # define leisure in [0,1] for each agent

This syntax is especially convenient, as it allows us to define vectors of parameters, each satisfying the natural inequality constraints. Next, we define the budget constraint, which also follows this convenient syntax:

 @addConstraint(m, c[i=1:N] .== (1.0-t)*(1.0-l[i]).*w[i] + e[i] )        # each agent must satisfy the budget constraint

Finally, we define a scalar-valued objective function, which is the sum of each individual’s utility:

 @setNLObjective(m, Max, sum{ g*log(c[i]) + (1-g)*log(l[i]) , i=1:N } )  # maximize the sum of utility across all agents

Notice that we can optimize one objective function instead of optimizing $N$ objective functions because the individual constrained maximization problems are independent across individuals, so the maximum of the sum is the sum of the maxima. Finally, we can apply the solver to this model and extract optimal consumption and leisure as follows:

 status = solve(m)                                                       # run numerical optimization c_opt = getValue(c)                                                     # extract demand for c l_opt = getValue(l)                                                     # extract demand for l

To make sure it worked, we compare the consumption extracted from this numerical approach to the consumption we generated previously using the true demand functions:

cor(c_opt,array(df[:consump]))
0.9999999998435865

Thus, we consumption values produced by the numerically optimizer’s approximation to the demand for consumption are almost identical to those produced by the true demand for consumption. Putting it all together, we create a function that can solve for optimal consumption and leisure given any particular values of $\gamma$ , $\tau$ , and $\epsilon$ :

 function hh_constrained_opt(g,t,w,e)      m = Model(solver=IpoptSolver())                                         # define empty model solved by Ipopt algorithm
  @defVar(m, c[i=1:N] >= 0)                                               # define positive consumption for each agent
  @defVar(m, 0 <= l[i=1:N] <= 1)                                          # define leisure in [0,1] for each agent
  @addConstraint(m, c[i=1:N] .== (1.0-t)*(1.0-l[i]).*w[i] + e[i] )        # each agent must satisfy the budget constraint
  @setNLObjective(m, Max, sum{ g*log(c[i]) + (1-g)*log(l[i]) , i=1:N } )  # maximize the sum of utility across all agents
  status = solve(m)                                                       # run numerical optimization
  c_opt = getValue(c)                                                     # extract demand for c
  l_opt = getValue(l)                                                     # extract demand for l
  demand = DataFrame(c_opt=c_opt,l_opt=l_opt)                             # return demand as DataFrame
end

hh_constrained_opt(gamma,tau,array(df[:wage]),array(df[:epsilon]))          # verify that it works at the true values of gamma, tau, and epsilon

5. Parallelized estimation by the Method of Simulated Moments

The replication codes for this section are available here.

We saw in the previous section that, for a given set of model parameters $\gamma$ and $\tau$ and a given draw of $\epsilon_{i}$ for each $i$ , we have enough information to simulation $c_{i}$ and $l_{i}$ , for each $i$ . Denote these simulated values by $\hat{c}_{i}\left(\epsilon;\gamma,\tau\right)$ and $\hat{l}_{i}\left(\epsilon;\gamma,\tau\right)$ . With these, we can define the moments,

$\hat{m}\left(\gamma,\tau\right)=\mathbb{E}_{\epsilon}\left[\begin{array}{c} \frac{1}{N}\sum_{i}\left[\hat{c}_{i}\left(\epsilon\right)-c_{i}\right]\\ \frac{1}{N}\sum_{i}\left[\hat{l}_{i}\left(\epsilon\right)-l_{i}\right] \end{array}\right]$

which is equal to zero under the model assumptions. A method of simulated moments (MSM) approach to estimate $\gamma$ and $\tau$ is then,

$\left(\hat{\gamma},\hat{\tau}\right)=\arg\min_{\gamma\in\left[0,1\right],\tau\in\left[0,1\right]}\hat{m}\left(\gamma,\tau\right)'W\hat{m}\left(\gamma,\tau\right)$

where $W$ is a $2\times2$ weighting matrix, which is only relevant when the number of moments is greater than the number of parameters, which is not true in our case, so $W$ can be ignored and the method of simulated moments simplifies to,

$\left(\hat{\gamma},\hat{\tau}\right)=\arg\min_{\gamma\in\left[0,1\right],\tau\in\left[0,1\right]}\left\{ \mathbb{E}_{\epsilon}\left[\frac{1}{N}\sum_{i}\left[\hat{c}_{i}\left(\epsilon\right)-c_{i}\right]\right]\right\} ^{2}+\left\{ \mathbb{E}_{\epsilon}\left[\frac{1}{N}\sum_{i}\left[\hat{l}_{i}\left(\epsilon\right)-l_{i}\right]\right]\right\} ^{2}$

Assuming we know the distribution of $\epsilon_i$ , we can simply draw many values of $\epsilon_i$ for each $i$ , and average the moments together across all of the draws of $\epsilon_i$ . This is Monte Carlo numerical integration. In Julia, we can create this objective function with a random draw of $\epsilon$ as follows:

function sim_moments(params)
  this_epsilon = randn(N)                                                     # draw random epsilon
  ggamma,ttau = params                                                        # extract gamma and tau from vector
  this_demand = hh_constrained_opt(ggamma,ttau,array(df[:wage]),this_epsilon) # obtain demand for c and l
  c_moment = mean( this_demand[:c_opt] ) - mean( df[:consump] )               # compute empirical moment for c
  l_moment = mean( this_demand[:l_opt] ) - mean( df[:leisure] )               # compute empirical moment for l
  [c_moment,l_moment]                                                         # return vector of moments
end

In order to estimate $\hat{m}\left(\gamma,\tau\right)$ , we need to run sim_moments(params) many times and take the unweighted average across them to achieve the expectation across $\epsilon_i$ . Because each calculation is computer-intensive, it makes sense to compute the contribution of $\hat{m}\left(\gamma,\tau\right)$ for each draw of $\epsilon_i$ on a different processor and then average across them.

Previously, I presented a convenient approach for parallelization in Julia. The idea is to initialize processors with the addprocs() function in an “outer” script, then import all of the needed data and functions to all of the different processors with the require() function applied to an “inner” script, where the needed data and functions are already managed by the inner script. This is incredibly easy and much simpler than the manual spawn-and-fetch approaches suggested by Julia’s official documentation.

In order to implement the parallelized method of simulated moments, the function hh_constrained_opt() and sim_moments() are stored in a file called est_msm_inner.jl. The following code defines the parallelized MSM and then minimizes the MSM objective using the optimize command set to use the Nelder-Mead algorithm from the Optim package:

####### Prepare for Parallelization #########

addprocs(3)                   # Adds 3 processors in parallel (the first is added by default)
print(nprocs())               # Now there are 4 active processors
require("est_msm_inner.jl")   # This distributes functions and data to all active processors

####### Define Sum of Squared Residuals in Parallel #########

function parallel_moments(params)
  params = exp(params)./(1.0+exp(params))   # rescale parameters to be in [0,1]
  results = @parallel (hcat) for i=1:numReps
    sim_moments(params)
  end
  avg_c_moment = mean(results[1,:])
  avg_l_moment = mean(results[2,:])
  SSR = avg_c_moment^2 + avg_l_moment^2
end

####### Minimize Sum of Squared Residuals in Parallel #########

using Optim
function MSM()
  out = optimize(parallel_moments,[0.,0.],method=:nelder_mead,ftol=1e-8)
  println(out)                                       # verify convergence
  exp(out.minimum)./(1.0+exp(out.minimum))           # return results in rescaled units
end

Parallelization is performed by the @parallel macro, and the results are horizontally concatenated from the various processors by the hcat command. The key tuning parameter here is numReps, which is the number of draws of $\epsilon$ to use in the Monte Carlo numerical integration. Because this example is so simple, a small number of repetitions is sufficient, while a larger number would be needed if $\epsilon$ entered the model in a more complicated manner. The process is run as follows and requires 268 seconds to run on my Macbook Air:

numReps = 12                                         # set number of times to simulate epsilon
gamma_MSM, tau_MSM = MSM()                           # Perform MSM
gamma_MSM
0.49994494921381816
tau_MSM
0.19992279518894465

Finally, given the MSM estimates of $\gamma$ and $\tau$ , we define the numerical derivative, $\frac{df(x)}{dx} \approx \frac{f(x+h)-f(x-h)}{2h}$ , for some small $h$ , as follows:

function Dconsump_Dtau(g,t,h)
  opt_plus_h = hh_constrained_opt(g,t+h,array(df[:wage]),array(df[:epsilon]))
  opt_minus_h = hh_constrained_opt(g,t-h,array(df[:wage]),array(df[:epsilon]))
  (mean(opt_plus_h[:c_opt]) - mean(opt_minus_h[:c_opt]))/(2*h)
end

barpsi_MSM = Dconsump_Dtau(gamma_MSM,tau_MSM,.1)
-5.016610457903023

Thus, we estimate the policy parameter $\bar\psi$ to be approximately $-5.017$ on average, while the true value is $\bar\psi = -\gamma \bar{w} = -(1/2)\times 10=-5$ , so the econometrician’s problem is successfully solved.

Bradley Setzler

Selection Bias Corrections in Julia, Part 1

By: Bradley Setzler

Re-posted from: https://juliaeconomics.com/2014/09/02/selection-bias-corrections-in-julia-part-1/

Selection bias arises when a data sample is not a random draw from the population that it is intended to represent. This is especially problematic when the probability that a particular individual appears in the sample depends on variables that also affect the relationships we wish to study. Selection bias corrections based on models of economic behavior were pioneered by the economist James J. Heckman in his seminal 1979 paper.

For an example of selection bias, suppose we wish to study the effectiveness of a treatment (a new medicine for patients with a particular disease, a preschool curriculum for children facing particular disadvantages, etc.). A random sample is drawn from the population of interest, and the treatment is randomly assigned to a subset of this sample, with the remaining subset serving as the untreated (“control”) group. If the subsets followed instructions, then the resulting data would serve as a random draw from the data generating process that we wish to study.

However, suppose the treatment and control groups do not comply with their assignments. In particular, if only some of the treated benefit from treatment while the others are in fact harmed by treatment, then we might expect the harmed individuals to leave the study. If we accepted the resulting data as a random draw from the data generating process, it would appear that the treatment was much more successful than it actually was; an individual who benefits is more likely to be present in the data than one who does not benefit.

Conversely, if treatment were very beneficial, then some individuals in the control group may find a way to obtain treatment, possibly without our knowledge. The benefits received by the control group would make it appear that the treatment was less beneficial than it actually was; the receipt of treatment is no longer random.

In this tutorial, I present some parameterized examples of selection bias. Then, I present examples of parametric selection bias corrections, evaluating their effectiveness in recovering the data generating processes. Along the way, I demonstrate the use of the GLM package in Julia. A future tutorial demonstrates non-parametric selection bias corrections.

Example 1: Selection on a Normally-Distributed Unobservable

Suppose that we wish to study of the effect of the observable variable $X_{i}$ on $Y_i$ . The data generating process is given by,

$Y_i=\beta_0+X_i\beta_1+\epsilon_i$ ,

where $X_i$ and $\epsilon_i$ are independent in the population. Because of this independence condition, the ordinary least squares estimator would be unbiased if the data $(Y,X)$ were drawn randomly from the population. However, suppose that the probability that individual $i$ were in the data set $\mathcal{S}$ were a function of $X$ and $\epsilon$ . For example, suppose that,

$\Pr\left( i \in \mathcal{S}\Big| X_i,\epsilon_i\right)=1$ if $X_i > \epsilon_i$ ,

and the probability is zero otherwise. This selection rule ensures that, among the individuals in the data (the $i$ in $\mathcal{S}$ ), the covariance between $X$ and $\epsilon$ will be positive, even though the covariance is zero in the population. When $X$ covaries positively with $\epsilon$ , then the OLS estimate of $\beta_1$ is biased upward, i.e., the OLS estimator converges to a value that is greater than $\beta_1$ .

To see the problem, consider the following simulation of the above process in which $X$ and $\epsilon$ are drawn as independent standard normal random variables:

srand(2)
N = 1000
X = randn(N)
epsilon = randn(N)
beta_0 = 0.
beta_1 = 1.
Y = beta_0 + beta_1.*X + epsilon
populationData = DataFrame(Y=Y,X=X,epsilon=epsilon)
selected = X.>epsilon
sampleData = DataFrame(Y=Y[selected],X=X[selected],epsilon=epsilon[selected])

There are 1,000 individuals in the population data, but 492 of them are selected to be included in the sample data. The covariance between X and epsilon in the population data is,

cov(populationData[:X],populationData[:epsilon])
0.00861456704877879

which is approximately zero, but in the sample data, it is,

cov(sampleData[:X],sampleData[:epsilon])
0.32121357192108513

which is approximately 0.32.

Now, we regress $Y$ on $X$ with the two data sets to obtain,

linreg(array(populationData[:X]),array(populationData[:Y]))
2-element Array{Float64,1}:
 -0.027204
  1.00882

linreg(array(sampleData[:X]),array(sampleData[:Y]))
2-element Array{Float64,1}:
 -0.858874
  1.4517

where, in Julia 0.3.0, the command array() replaces the old command matrix() in converting a DataFrame into a numerical Array. This simulation demonstrates severe selection bias associated with using the sample data to estimate the data generating process instead of the population data, as the true parameters, $\beta_0=0,\beta_1=1$ , are not recovered by the sample estimator.

Correction 1: Heckman (1979)

The key insight of Heckman (1979) is that the correlation between $X$ and $\epsilon$ can be represented as an omitted variable in the OLS moment condition,

$\mathbb{E}\left[Y_i\Big|X_i,i\in\mathcal{S}\right]=\mathbb{E}\left[\beta_0 + \beta_1X_i+\epsilon_i\Big|X_i,i\in\mathcal{S}\right]=\beta_0 + \beta_1X_i+\mathbb{E}\left[\epsilon_i\Big|X_i,i\in\mathcal{S}\right]$ ,

Furthermore, using the conditional density of the standard Normally distributed $\epsilon$ ,

$\mathbb{E}\left[\epsilon_i\Big|X_i,i\in\mathcal{S}\right]=\mathbb{E}\left[\epsilon_i\Big|X_i,X_i>\epsilon_i\right]=\frac{-\phi\left(X_i\right)}{\Phi\left(X_i\right)}$ .

which is called the inverse Mills ratio, where $\phi$ and $\Phi$ are the probability and cumulative density functions of the standard normal distribution. As a result, the moment condition that holds in the sample is,

$\mathbb{E}\left[Y_i\Big|X_i,i\in\mathcal{S}\right]=\beta_0 + \beta_1X_i+\frac{-\phi\left(X_i\right)}{\Phi\left(X_i\right)}$

Returning to our simulation, the inverse Mills ratio is added to the sample data as,

sampleData[:invMills] = -pdf(Normal(),sampleData[:X])./cdf(Normal(),sampleData[:X])

Then, we run the regression corresponding to the sample moment condition,

linreg(array(sampleData[[:X,:invMills]]),array(sampleData[:Y]))
3-element Array{Float64,1}:
 -0.166541
  1.05648
  0.827454

We see that the estimate for $\beta_1$ is now 1.056, which is close to the true value of 1, compared to the non-corrected estimate of 1.452 above. Similarly, the estimate for $\beta_0$ has improved from -0.859 to -0.167, when the true value is 0. To see that the Heckman (1979) correction is consistent, we can increase the sample size to $N=100,000$ , which yields the estimates,

linreg(array(sampleData[[:X,:invMills]]),array(sampleData[:Y]))
3-element Array{Float64,1}:
 -0.00417033
  1.00697
  0.991503

which are very close to the true parameter values.

Note that this analysis generalizes to the case in which $X$ contains $K$ variables and the selection rule is,

$\delta_0 + \delta_1 X_1 + \delta_2 X_2 + \ldots + \delta_K X_k > \epsilon$ ,

which is the case considered by Heckman (1979). The only difference is that the coefficients $\delta_k$ must first be estimated by regressing an indicator for $i \in \mathcal{S}$ on $X$ , then using the fitted equation within the inverse Mills ratio. This requires that we observe $X$ for $i \notin \mathcal{S}$ . Probit regression is covered in a slightly different context below.

As a matter of terminology, the process of estimating $\delta$ is called the “first stage”, and estimating $\beta$ conditional on the estimates of $\delta$ is called the “second stage”. When the coefficient on the inverse Mills ratio is positive, it is said that “positive selection” has occurred, with “negative selection” otherwise. Positive selection means that, without the correction, the estimate of $\beta_1$ would have been upward-biased, while negative selection results in a downward-biased estimate. Finally, because the selection rule is driven by an unobservable variables $\epsilon$ , this is a case of “selection on unobservables”. In the next section we consider a case of “selection on observables”.

Example 2: Probit Selection on Observables

Suppose that we wish to know the mean and variance of $Y$ in the population. However, our sample of $Y$ suffers from selection bias. In particular, there is some $X$ such that the probability of observing $Y$ depends on $X$ according to,

$\Pr\left(i\in\mathcal{S}\Big| X_i\right)=F\left(X_i\right)$ ,

where $F$ is some function with range $[0,1]$ . Notice that, if $Y$ and $X$ were independent, then the resulting sample distribution of $Y$ would be a random draw from the population (marginal distribution) of $Y$ . Instead, we suppose $\mathrm{Cov}\left(X,Y\right)\neq 0$ . For example,

srand(2)
N = 10000
populationData = DataFrame(rand(MvNormal([0,0.],[1 .5;.5 1]),N)')
names!(populationData,[:X,:Y])

mean(array(populationData),1)
1x2 Array{Float64,2}:
 -0.0281916  -0.022319

cov(array(populationData))
2x2 Array{Float64,2}:
 0.98665   0.500912
 0.500912  1.00195

In this simulated population, the estimated mean and variance of $Y$ are -0.022 and 1.002, and the covariance between $X$ and $Y$ is 0.501. Now, suppose the probability that $Y_i$ is observed is a probit regression of $X_i$ ,

$\Pr\left( i\in\mathcal{S}\Big| X_i \right) = \Phi\left( \beta_0 + \beta_1 X_i \right)$ ,

where $\Phi$ is the CDF of the standard normal distribution. Letting $D_i=1$ indicate that $i \in \mathcal{S}$ , we can generate the sample selection rule $D$ as,

beta_0 = 0
beta_1 = 1
index = (beta_0 + beta_1*data[:X])
probability = cdf(Normal(0,1),index)
D = zeros(N)
for i=1:N
    D[i] = rand(Bernoulli(probability[i]))
end
populationData[:D] = D
sampleData = populationData
sampleData[D.==0,:Y] = NA

The sample data has missing values in place of $Y_i$ if $D_i=0$ . The estimated mean and variance of $Y$ in the sample data are 0.275 (which is too large) and 0.862 (which is too small).

Correction 2: Inverse Probability Weighting

The reason for the biased estimates of the mean and variance of $Y$ in Example 2 is sample selection on the observable $X$ . In particular, certain values of $Y$ are over-represented due to their relationship with $X$ . Inverse probability weighting is a way to correct for the over-representation of certain types of individuals, where the “type” is captured by the probability of being included in the sample.

In the above simulation, conditional on appearing in the population, the probability that an individual of type $X_i=1$ is included in the sample is 0.841. By contrast, the probability that an individual of type $X_i=0$ is included in the sample is 0.5, so type $X_i$ is over-represented by a factor of 0.841/0.5 = 1.682. If we could reduce the impact that type $X_i=1$ has in the computation of the mean and variance of $Y$ by a factor of 1.682, we would alter the balance of types in the sample to match the balance of types in the population. Inverse probability weighting generalizes this logic by weighting each individual’s impact by the inverse of the probability that this individual appears in the sample.

Before we can make the correct, we must first estimate the probability of sample inclusion. This can be done by fitting the probit regression above by least-squares. For this, we use the GLM package in Julia, which can be installed the usual way with the command Pkg.add(“GLM”).

using GLM
Probit = glm(D ~ X, sampleData, Binomial(), ProbitLink())
DataFrameRegressionModel{GeneralizedLinearModel,Float64}:

Coefficients:
             Estimate Std.Error  z value Pr(>|z|)
(Intercept)  0.114665  0.148809 0.770554   0.4410
X             1.14826   0.21813  5.26414    1e-6

estProb = predict(Probit)
weights = 1./estProb[D.==1]/sum(1./estProb[D.==1])

which are the inverse probability weights needed to match the sample distribution to the population distribution.

Now, we use the inverse probability weights to correct the mean and variance estimates of $Y$ ,

correctedMean = sum(sampleData[D.==1,:Y].*weight)
-0.024566923132025013

correctedVariance = (N/(N-1))*sum((sampleData[D.==1,:Y]-correctedMean).^2.*weight)
1.0094029613131092

which are very close to the population values of -0.022319 and 1.00195. The logic here extends to the case of multivariate $X$ , as more coefficients are added to the Probit regression. The logic also extends to other functional forms of $F$ , for example, switching from Probit to Logit is achieved by replacing the ProbitLink() with LogitLink() in the glm() estimation above.

Example 3: Generalized Roy Model

For the final example of this tutorial, we consider a model which allows for rich, realistic economic behavior. In words, the Generalized Roy Model is the economic representation of a world in which each individual must choose between two options, where each option has its own benefits, and one of the options costs more than the other. In math notation, the first alternative, denoted $D_i=1$ , relates the outcomes $Y_i$ to the individual’s observable characteristics, $X_i$ , by,

$Y_{1,i} = \mu_1\left(X_i\right)+U_{1,i}$ .

Similarly, the second alternative, denoted $D_i=0$ , relates $Y_i$ to $X_i$ , by,

$Y_{0,i} = \mu_0\left(X_i\right)+U_{0,i}$ .

The value of $Y_i$ that appears in our sample is thus given by,

$Y_i = D_iY_{1,i} + (1-D_i)Y_{0,i}$ .

Finally, the value of $D_i$ is chosen by individual $i$ according to,

$D_i=1$ if $Y_{1,i}-Y_{0,i}-C_i>0$ ,

where $C_i$ is the cost of choosing the alternative $D_i=1$ and is given by,

$C_i = \mu_C\left(X_i,Z_i\right)+U_{C,i}$ ,

where $Z$ contains additional characteristics of $i$ that are not included in $X$ .

We assume that the data only contains $Y_i,D_i,X_i,Z_i$ ; it does not contain the variables $Y_{i,1},Y_{i,0},U_{i,1},U_{i,0},U_{i,C}$ or the functions $\mu_1,\mu_0,\mu_C$ . Assuming that the three $\mu$ functions follow the linear form and that the unobservables $U$ are independent and Normally distributed, we can simulate the data generating process as,

srand(2)
N = 1000
sampleData = DataFrame(rand(MvNormal([0,0.],[1 .5; .5 1]),N)')
names!(sampleData,[:X,:Z])
U1 = rand(Normal(0,.5),N)
U0 = rand(Normal(0,.7),N)
UC = rand(Normal(0,.9),N)
betas1 = [0,1]
betas0 = [.3,.2]
betasC = [.1,.1,.1]
Y1 = betas1[1] + betas1[2].*sampleData[:X] + U1
Y0 = betas0[1] + betas0[2].*sampleData[:X] + U0
C = betasC[1] + betasC[2].*sampleData[:X] + betasC[3].*sampleData[:Z] + UC
D = Y1-Y0-C.>0
Y = D.*Y1 + (1-D).*Y0
sampleData[:D] = D
sampleData[:Y] = Y

In this simulation, about 38% of individuals choose the alternative $D_i=1$ . About 10% of individuals choose $D_i=0$ even though they receive greater benefits under $D_i=1$ due to the high cost $C_i$ associated with $D_i=1$ .

Solution 3: Heckman Correction for Generalized Roy Model

The identification of this model is attributable to Heckman and Honore (1990). Estimation proceeds in steps. The first step is to notice that the left- and right-hand terms in the following moment equation motivate a Probit regression:

$\mathbb{E}\left[D_i\Big|X_i,Z_i\right]=\Pr\left(\mu_D\left(X_i,Z_i\right)>U_{D,i}\Big|X_i,Z_i\right)=\Phi\left(\mu_D\left(X_i,Z_i\right)\right)$ ,

where $U_{D,i}\equiv -\left(U_{1,i}-U_{0,i}-U_{C,i}\right)/\sigma_D\sim\mathcal{N}\left(0,1\right)$ is the negative of the total error term arising in the equation that determines $D_i$ above, $\sigma_D \equiv \sqrt{\mathrm{Var}\left(U_{1,i}-U_{0,i}-U_{C,i}\right)}$ , and,

$\mu_D\left(X,Z\right) \equiv \left([1,X]\beta_1 -[1,X]\beta_0 -[1,X,Z]\beta_C\right)/\sigma_D \equiv [1,X,Z]\beta_D$ ,

In the simulation above, $\beta_D = [-.4,.7,-.1]/\sqrt{.5+.7+.9}\approx[-0.276,0.483,-0.069]$ . We can estimate $\beta_D$ from the Probit regression of $D$ on $X$ and $Z$ .

betasD = coef(glm(D~X+Z,sampleData,Binomial(),ProbitLink()))
3-element Array{Float64,1}:
 -0.299096
  0.59392 
 -0.103155

Next, notice that,

$\mathbb{E}\left[Y_i\Big|D_i=1,X_i,Z_i\right] =[1,X_i]\beta_1+\mathbb{E}\left[U_{1,i}\Big|D_i=1,X_i,Z_i\right]$ ,

where,

$\mathbb{E}\left[U_{1,i}\Big|D_i=1,X_i,Z_i\right] =\mathbb{E}\left[U_{1,i}\Big|\mu_D\left(X_i,Z_i\right)>U_{i,D},X_i,Z_i\right]=\rho_1 \frac{-\phi\left(\mu_D\left(X_i,Z_i\right)\right)}{\Phi\left(\mu_D\left(X_i,Z_i\right)\right)}$ ,

which is the inverse Mills ratio again, where $\rho_1 \equiv \frac{\mathrm{Cov}\left(U_1,U_D\right)}{\mathrm{Var}\left(U_D\right)}$ . Substituting in the estimate for $\beta_D$ , we consistently estimate $\beta_1$ :

fittedVals = hcat(ones(N),array(sampleData[[:X,:Z]]))*betasD

sampleData[:invMills1] = -pdf(Normal(0,1),fittedVals)./cdf(Normal(0,1),fittedVals)

correctedBetas1 = linreg(array(sampleData[D,[:X,:invMills1]]),vec(array(sampleData[D,[:Y]])))
3-element Array{Float64,1}:
  0.0653299
  0.973568 
 -0.135445

To see how well the correction has performed, compare these estimates to the uncorrected estimates of $\beta_1$ ,

biasedBetas1 = linreg(array(sampleData[D,[:X]]),vec(array(sampleData[D,[:Y]])))
2-element Array{Float64,1}:
 0.202169
 0.927317

Similar logic allows us to estimate $\beta_0$ :

sampleData[:invMills0] = pdf(Normal(0,1),fittedVals)./(1-cdf(Normal(0,1),fittedVals))

correctedBetas0 = linreg(array(sampleData[D.==0,[:X,:invMills0]]),vec(array(sampleData[D.==0,[:Y]])))
3-element Array{Float64,1}:
 0.340621
 0.207068
 0.323793

biasedBetas0 = linreg(array(sampleData[D.==0,[:X]]),vec(array(sampleData[D.==0,[:Y]])))
2-element Array{Float64,1}:
 0.548451
 0.295698

In summary, we can consistently estimate the benefits associated with each of two alternative choices, even though we only observe each individual in one of the alternatives, subject to heavy selection bias, by extending the logic introduced by Heckman (1979).

Bradley J. Setzler

Cobbling together parallel random number generation in Julia

I’m starting to work on some computationally demanding projects, (Monte Carlo simulations of bootstraps of out-of-sample forecast comparisons) so I thought I should look at Julia some more. Unfortunately, since Julia’s so young (it’s almost at version 0.3.0 as I write this) a lot of code still needs to be written. Like Random Number Generators (RNGs) that work in parallel. So this post describes an approach that parallelizes computation using a standard RNG; for convenience I’ve put the code (a single function) is in a grotesquely ambitiously named package on GitHub: ParallelRNGs.jl. (Also see this thread on the Julia Users mailing list.)

A few quick points about RNGs and simulations. Most econometrics papers have a section that examines the performance of a few estimators in a known environment (usually the estimators proposed by the paper and a few of the best preexisting estimators). We do this by simulating data on a computer, using that data to produce estimates, and then comparing those estimate to the parameters they’re estimating. Since we’ve generated the data ourselves, we actually know the true values of those parameters, so we can make a real comparison. Do that for 5000 simulated data sets and you can get a reasonably accurate view of how the statistics might perform in real life.

For many reasons, it’s useful to be able to reproduce the exact same simulations again in the future. (Two obvious reasons: it allows other researchers to be able to reproduce your results, and it can make debugging much faster when you discover errors.) So we almost always use pseudo Random Number Generators that use a deterministic algorithm to produce a stream of numbers that behaves in important ways like a stream of independent random values. You initialize these RNGs by setting a starting value (the “pseudo” aspect of the RNGs is implicit from now on) and anyone who has that starting value can reproduce the identical sequence of numbers that you generated. A popular RNG is the “Mersenne Twister,” and “popular” is probably an understatement: it’s the default RNG in R, Matlab, and Julia. And (from what I’ve read; this isn’t my field at all) it’s well regarded for producing a sequence of random numbers for statistical simulations.

But it’s not necessarily appropriate for producing several independent sequences of random numbers. Which is vitally important because I have an 8 core workstation that needs to run lots of simulations, and I’d like to execute 1/8th of the total simulations on each of its cores.

There’s a common misconception that you can get independent random sequences just by choosing different initial values for each sequence, but that’s not guaranteed to be true. There are algorithms for choosing different starting values that are guaranteed to produce independent streams for the Mersenne Twister (see this research by one of the MT’s inventors), but they aren’t implemented in Julia yet. (Or in R, as far as I can tell; they use a different RNG for parallel applications.) And it turns out that Mersenne Twister is the only RNG that’s included in Julia so far.

So, this would be a perfect opportunity for me to step up and implement some of these advanced algorithms for the Mersenne Twister. Or to implement some of the algorithms developed by L’Ecuyer and his coauthors, which are what R uses. And there’s already C code for both options.

But I haven’t done that yet. I’m ~~lazy~~ busy.

Instead, I’ve written an extremely small function that wraps Julia’s default RNG, calls it from the main process alone to generate random numbers, and then sends those random numbers to each of the other processes/cores where the rest of the simulation code runs. The function’s really simple:

function replicate(sim::Function, dgp::Function, n::Integer)
    function rvproducer()
        for i=1:n
            produce(dgp())
        end
    end
    return(pmap(sim, Task(rvproducer)))
end

That’s all. If you’re not used to Julia, you can ignore the “::Function” and the “::Integer” parts of the arguments. Those just identify the datatype of the argument and you can read it as “dgp_function” if you want (and explicitly providing the types like this is optional anyway). So, you give “replicate” two functions: “dgp” generates the random numbers and “sim” does the remaining calculations; “n” is the number of simulations to do. All of the work is done in “pmap” which parcels out the random numbers and sends them to different processors. (There’s a simplified version of the source code for pmap at that link.)

And that’s it. Each time a processor finishes one iteration, pmap calls dgp() again to generate more random numbers and passes them along. It automatically waits for dgp() to finish, so there are no race conditions and it produces the exact same sequence of random numbers every time. The code is shockingly concise. (It shocked me! I wrote it up assuming it would fail so I could understand pmap better and I was pretty surprised when it worked.)

A quick example might help clear up it’s usage. We’ll write a DGP for the bootstrap:

const n = 200     #% Number of observations for each simulation
const nboot = 299 #% Number of bootstrap replications
addprocs(7)       #% Start the other 7 cores
dgp() = (randn(n), rand(1:n, (n, nboot)))

The data are iid Normal, (the “randn(n)” component) and it’s an iid nonparametric bootstrap (the “rand(1:n, (n, nboot))”, which draws independent values from 1 to n and fills them into an n by nboot matrix). Oh, and there’s a good reason for those weird “#%” comments; “#” is Julia’s comment character, but WordPress doesn’t support syntax highlighting for Julia, so we’re pretending this is Matlab code. And “%” is Matlab’s comment character, which turns the comment green.

We’ll use a proxy for some complicated processing step:

@everywhere function sim(x)
    nboot = size(x[2], 2)
    bootvals = Array(Float64, nboot)
    for i=1:nboot
        bootvals[i] = mean(x[1][x[2][:,i]])
    end
    confint = quantile(bootvals, [0.05, 0.95])
    sleep(3) #% not usually recommended!
    return(confint[1] < 0 < confint[2])
end

So “sim” calculates the mean of each bootstrap sample and calculates the 5th and 95th percentile of those simulated means, giving a two-sided 90% confidence interval for the true mean. Then it checks whether the interval contains the true mean (0). And it also wastes 3 seconds sleeping, which is a proxy for more complicated calculations but usually shouldn’t be in your code. The initial “@everywhere” is a Julia macro that loads this function into each of the separate processes so that it’s available for parallelization. (This is probably as good a place as any to link to Julia’s “Parallel Computing” documentation.)

Running a short Monte Carlo is simple:

julia> srand(84537423); #% Initialize the default RNG!!!
julia> @time mc1 = mean(replicate(sim, dgp, 500))

elapsed time: 217.705639 seconds (508892580 bytes allocated, 0.13% gc time)
0.896 #% = 448/500

So, about 3.6 minutes and the confidence intervals have coverage almost exactly 90%.

It’s also useful to compare the execution time to a purely sequential approach. We can do that by using a simple for loop:

function dosequential(nsims)
    boots = Array(Float64, nsims)
    for i=1:nsims
        boots[i] = sim(dgp())
    end
    return boots
end

And, to time it:

julia> dosequential(1); #% Force compilation before timing
julia> srand(84537423); #% Reinitialize the default RNG!!!
julia> @time mc2 = mean(dosequential(500))

elapsed time: 1502.038961 seconds (877739616 bytes allocated, 0.03% gc time)
0.896 #% = 448/500

This takes a lot longer: over 25 minutes, 7 times longer than the parallel approach (exactly what we’d hope for, since the parallel approach runs the simulations on 7 cores). And it gives exactly the same results since we started the RNG at the same initial value.

So this approach to parallelization is great… sometimes.

This approach should work pretty well when there aren’t that many random numbers being passed to each processor, and when there aren’t that many simulations being run; i.e. when “sim” is an inherently complex calculation. Otherwise, the overhead of passing the random numbers to each process can start to matter a lot. In extreme cases, “dosequential” can be faster than “replicate” because the overhead of managing the simulations and passing around random variables dominates the other calculations. In those applications, a real parallel RNG becomes a lot more important.

If you want to play with this code yourself, I made a small package for the replicate function: ParallelRNGs.jl on GitHub. The name is misleadingly ambitious (ambitiously misleading?), but if I do add real parallel RNGs to Julia, I’ll put them there too. The code is still buggy, so use it at your own risk and let me know if you run into problems. (Filing an issue on GitHub is the best way to report bugs.)

P.S. I should mention again that Julia is an absolute joy of a language. Package development isn’t quite as nice as in Clojure, where it’s straightforward to load and unload variables from the package namespace (again, there’s lots of code that still needs to be written). But the actual language is just spectacular and I’d probably want to use it for simulations even if it were slow. Seriously: seven lines of new code to get an acceptable parallel RNG.

Filed under: Blog Tagged: econometrics, julia, programming

juliabloggers.com

A Julia Language Blog Aggregator