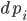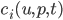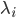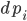Re-posted from: http://www.stochasticlifestyle.com/gpu-accelerated-ode-solving-in-r-with-julia-the-language-of-libraries/
R is a widely used language for data science, but due to performance most of its underlying library are written in C, C++, or Fortran. Julia is a relative newcomer to the field which has busted out since its 1.0 to become one of the top 20 most used languages due to its high performance libraries for scientific computing and machine learning. Julia’a value proposition has been its high performance in high level language, known as solving the two language problem, which has allowed allowed the language to build a robust, mature, and expansive package ecosystem. While this has been a major strength for package developers, the fact remains that there are still large and robust communities in other high level languages like R and Python. Instead of spawning distracting language wars, we should ask the question: can Julia become a language of libraries to accelerate these other languages as well?
This is definitely not the first time this question was asked. The statistics libraries in Julia were developed by individuals like Douglas Bates who built some of R’s most widely used packages like lme4, Bioconductor, and Matrix. Doug had written a blog post in 2018 showing how to get top notch performance in linear mixed effects model fitting via JuliaCall. In 2018 the JuliaDiffEq organization had written a blog post demonstrating the use of DifferentialEquations.jl in R and Python (the Jupyter of Diffrential Equations). Now rebranded as SciML for Scientific Machine Learning, we looked to expand our mission and bring automated model discovery and acceleration include other languages like R and Python with Julia as the base.
With the release of diffeqr v1.0, we can now demonstrate many advances in R through the connection to Julia. Specifically, I would like to use this blog post to showcase:
- The new direct wrapping interface of diffeqr
- JIT compilation and symbolic analysis of ODEs and SDEs in R using Julia and ModelingToolkit.jl
- GPU-accelerated simulations of ensembles using Julia’s DiffEqGPU.jl
Together we will demonstrate how models in R can be accelerated by 1000x without a user ever having to write anything but R.
A Quick Note Before Continuing
Before continuing on with showing all of the features, I wanted to ask for support so that we can continue developing these bridged libraries. Specifically, I would like to be able to support developers interested in providing a fully automated Julia installation and static compilation so that calling into Julia libraries is just as easy as any Rcpp library. To show support, the easiest thing to do is to star our libraries. The work of this blog post is build on DifferentialEquations.jl, diffeqr, ModelingToolkit.jl, and DiffEqGPU.jl. Thank you for your patience and now back to our regularly scheduled program.
diffeqr v1.0: Direct wrappers for Differential Equation Solving in R
First let me start with the new direct wrappers of differential equations solvers in R. In the previous iterations of diffeqr, we had relied on specifically designed high level functions, like “ode_solve”, to compensate for the fact that one could not directly use Julia’s original DifferentialEquations.jl interface directly from R. However, the new diffeqr v1.0 directly exposes the entirety of the Julia library in an easy to use framework.
To demonstrate this, let’s see how to define the Lorenz ODE with diffeqr. In Julia’s DifferentialEquations.jl, we would start by defining an “ODEProblem” that contains the initial condition u0, the time span, the parameters, and the f in terms of `u’ = f(u,p,t)` that defines the derivative. In Julia, this would look like:
using DifferentialEquations function lorenz(du,u,p,t) du[1] = p[1]*(u[2]-u[1]) du[2] = u[1]*(p[2]-u[3]) - u[2] du[3] = u[1]*u[2] - p[3]*u[3] end u0 = [1.0,1.0,1.0] tspan = (0.0,100.0) p = [10.0,28.0,8/3] prob = ODEProblem(lorenz,u0,tspan,p) sol = solve(prob,saveat=1.0)
With the new diffeqr, diffeq_setup() is a function that does a few things:
- It instantiates a Julia process to utilize as its underlying compute engine
- It first checks if the correct Julia libraries are installed and, if not, it installs them for you
- Then it exposes all of the functions of DifferentialEquations.jl into its object
What this means is that the following is the complete diffeqr v1.0 code for solving the Lorenz equation is:
library(diffeqr)
de <- diffeqr::diffeq_setup()
f <- function(u,p,t) {
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
return(c(du1,du2,du3))
}
u0 <- c(1.0,1.0,1.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(f, u0, tspan, p)
sol <- de$solve(prob,saveat=1.0)
This then carries on through SDEs, DDEs, DAEs, and more. Through this direct exposing form, the whole library of DifferentialEquations.jl is at the finger tips of any R user, making it a truly cross-language platform.
(Note that the only caveat is that diffeq_setup requires that the user has already installed Julia and julia is included in the path. We hope that future developments can eliminate this need.)
JIT compilation and symbolic analysis of ODEs and SDEs in R via ModelingToolkit.jl
The reason for Julia is speed (well and other things, but here, SPEED!). Using the pure Julia library, we can solve the Lorenz equation 100 times in about 0.05 seconds:
@time for i in 1:100 solve(prob,saveat=1.0) end 0.048237 seconds (156.80 k allocations: 6.842 MiB) 0.048231 seconds (156.80 k allocations: 6.842 MiB) 0.048659 seconds (156.80 k allocations: 6.842 MiB)
Using diffeqr connected version, we get:
lorenz_solve <- function (i){
de$solve(prob,saveat=1.0)
}
> system.time({ lapply(1:100,lorenz_solve) })
user system elapsed
6.81 0.02 6.83
> system.time({ lapply(1:100,lorenz_solve) })
user system elapsed
7.09 0.00 7.10
> system.time({ lapply(1:100,lorenz_solve) })
user system elapsed
6.78 0.00 6.79
That’s not good, that’s about 100x difference! In this blog post I described that interpreter overhead and context switching are the main causes of this issue. We’ve also demonstrated that ML accelerators like PyTorch generally do not perform well in this regime since those kinds of accelerators rely on heavy array operations, unlike the scalarized nonlinear interactions seen in a lot of differential equation modeling. For this reason we cannot just slap any old JIT compiler onto the f call and then put it into the function since there would still be left over. So we need to do something a bit tricky.
In my JuliaCon 2020 talk, Automated Optimization and Parallelism in DifferentialEquations.jl I demonstrated how ModelingToolkit.jl can be used to trace functions and generate highly optimized sparse and parallel code for scientific computing all in an automated fashion. It turns out that JuliaCall can do a form of tracing on R functions, something that exploited to allow autodiffr to automatically differentiate R code with Julia’s AD libraries. Thus it turns out that the same modelingtoolkitization methods used in AutoOptimize.jl can be used on a subset of R codes which includes a large majority of differential equation models.
In short, we can perform automated acceleration of R code by turning it into sparse parallel Julia code. This was exposed in diffeqr v1.0 as the `jitoptimize_ode(de,prob)` function (also `jitoptimize_sde(de,prob)`). Let’s try it out on this example. All you need to do is give it the ODEProblem which you wish to accelerate. Let’s take the last problem and turn it into a pure Julia defined problem and then time it:
fastprob <- diffeqr::jitoptimize_ode(de,prob)
fast_lorenz_solve <- function (i){
de$solve(fastprob,saveat=1.0)
}
system.time({ lapply(1:100,fast_lorenz_solve) })
> system.time({ lapply(1:100,fast_lorenz_solve) })
user system elapsed
0.05 0.00 0.04
> system.time({ lapply(1:100,fast_lorenz_solve) })
user system elapsed
0.07 0.00 0.06
> system.time({ lapply(1:100,fast_lorenz_solve) })
user system elapsed
0.07 0.00 0.06
And there you go, an R user can get the full benefits of Julia’s optimizing JIT compiler without having to write lick of Julia code! This function also did a few other things, like automatically defined the Jacobian code to make implicit solving of stiff ODEs much faster as well, and it can perform sparsity detection and automatically optimize computations on that.
To see how much of an advance this is, note that this Lorenz equation is the same from the deSolve examples page. So let’s take their example and see how well it performs:
library(deSolve)
Lorenz <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
dX <- a * X + Y * Z
dY <- b * (Y - Z)
dZ <- -X * Y + c * Y - Z
list(c(dX, dY, dZ))
})
}
parameters <- c(a = -8/3, b = -10, c = 28)
state <- c(X = 1, Y = 1, Z = 1)
times <- seq(0, 100, by = 1.0)
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
desolve_lorenz_solve <- function (i){
state <- c(X = runif(1), Y = runif(1), Z = runif(1))
parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}
> system.time({ lapply(1:100,desolve_lorenz_solve) })
user system elapsed
5.03 0.03 5.07
>
> system.time({ lapply(1:100,desolve_lorenz_solve) })
user system elapsed
5.42 0.00 5.44
> system.time({ lapply(1:100,desolve_lorenz_solve) })
user system elapsed
5.41 0.00 5.41
Thus we see 100x acceleration over the leading R library without users having to write anything but R code. This is the true promise in action of a “language of libraries” helping to extend all other high level languages!
GPU-acceleration of ODEs in R via DiffEqGPU.jl
Can we go deeper? Yes we can. In many cases like in optimization and sensitivity analysis of models for pharmacology the users need to solve the same ODE thousands or millions of times to understand the behavior over a large parameter space. To solve this problem well in Julia, we built DiffEqGPU.jl which transforms the pure Julia function into a .ptx kernel to then parallelize the ODE solver over. What this looks like is the following solves the Lorenz equation 100,000 times with randomized initial conditions and parameters:
using DifferentialEquations, DiffEqGPU function lorenz(du,u,p,t) du[1] = p[1]*(u[2]-u[1]) du[2] = u[1]*(p[2]-u[3]) - u[2] du[3] = u[1]*u[2] - p[3]*u[3] end u0 = [1.0,1.0,1.0] tspan = (0.0,100.0) p = [10.0,28.0,8/3] prob = ODEProblem(lorenz,u0,tspan,p) prob_func = (prob,i,repeat) -> remake(prob,u0=rand(3).*u0,p=rand(3).*p) monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy=false) sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=100_000,saveat=1.0f0)
Notice how this is only two lines of code different from what we had before, and now everything is GPU accelerated! The requirement for this to work is that the ODE/SDE/DAE function has to be written in Julia… but diffeqr::jitoptimize_ode(de,prob) accelerates the ODE solving in R by generating a Julia function, so could that mean…?
Yes, it does mean we can use DiffEqGPU directly on ODEs defined in R. Let’s see this in action. Once again, we will write almost exactly the same code as in Julia, except with `de$` and with diffeqr::jitoptimize_ode(de,prob) to JIT compile our ODE definition. What this looks like is the following:
de <- diffeqr::diffeq_setup()
degpu <- diffeqr::diffeqgpu_setup()
lorenz <- function (u,p,t){
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
c(du1,du2,du3)
}
u0 <- c(1.0,1.0,1.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(lorenz,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)
prob_func <- function (prob,i,rep){
de$remake(prob,u0=runif(3)*u0,p=runif(3)*p)
}
ensembleprob = de$EnsembleProblem(fastprob, prob_func = prob_func, safetycopy=FALSE)
sol = de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=100000,saveat=1.0)
Note that diffeqr::diffeqgpu_setup() does the following:
- It sets up the drivers and installs the right version of CUDA for the user if not already available
- It installs the DiffEqGPU library
- It exposes the pieces of the DiffEqGPU library for the user to then call onto ensembles
This means that this portion of the library is fully automated, all the way down to the installation of CUDA! Let’s time this out a bit. 100,000 ODE solves in serial:
@time sol = solve(monteprob,Tsit5(),EnsembleSerial(),trajectories=100_000,saveat=1.0f0) 15.045104 seconds (18.60 M allocations: 2.135 GiB, 4.64% gc time) 14.235984 seconds (16.10 M allocations: 2.022 GiB, 5.62% gc time)
100,000 ODE solves on the GPU in Julia:
@time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=100_000,saveat=1.0f0) 2.071817 seconds (6.56 M allocations: 1.077 GiB) 2.148678 seconds (6.56 M allocations: 1.077 GiB)
Now let’s check R in serial:
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=100000,saveat=1.0) })
user system elapsed
24.16 1.27 25.42
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=100000,saveat=1.0) })
user system elapsed
25.45 0.94 26.44
and R on GPUs:
> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=100000,saveat=1.0) })
user system elapsed
12.39 1.51 13.95
> system.time({ de$solve(ensembleprob,de$Tsit5(),degpu$EnsembleGPUArray(),trajectories=100000,saveat=1.0) })
user system elapsed
12.55 1.36 13.90
R doesn’t reach quite the level of Julia here, and if you profile you’ll see it’s because the `prob_func`, i.e. the function that tells you which problems to solve, is still a function written in R and this becomes the bottleneck as the computation becomes faster and faster. Thus you will get closer and closer to the Julia speed with longer and harder ODEs, but it still means there’s work to be done. Another detail is that the Julia code is able to be further accelerated by using 32-bit numbers. Let’s see that in action:
using DifferentialEquations, DiffEqGPU function lorenz(du,u,p,t) du[1] = p[1]*(u[2]-u[1]) du[2] = u[1]*(p[2]-u[3]) - u[2] du[3] = u[1]*u[2] - p[3]*u[3] end u0 = Float32[1.0,1.0,1.0] tspan = (0.0f0,100.0f0) p = Float32[10.0,28.0,8/3] prob = ODEProblem(lorenz,u0,tspan,p) prob_func = (prob,i,repeat) -> remake(prob,u0=rand(Float32,3).*u0,p=rand(Float32,3).*p) monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy=false) @time sol = solve(monteprob,Tsit5(),EnsembleGPUArray(),trajectories=100_000,saveat=1.0f0) # 1.781718 seconds (6.55 M allocations: 918.051 MiB) # 1.873190 seconds (6.56 M allocations: 917.875 MiB)
Right now the Julia to R bridge converts all 32-bit numbers back to 64-bit numbers so this doesn’t seem to be possible without the user writing some Julia code, but we hope to get this fixed in one of our coming releases.
To figure out where that leaves us, let’s use deSolve to solve that same Lorenz equation 100 and 1,000 times:
library(deSolve)
Lorenz <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
dX <- a * X + Y * Z
dY <- b * (Y - Z)
dZ <- -X * Y + c * Y - Z
list(c(dX, dY, dZ))
})
}
parameters <- c(a = -8/3, b = -10, c = 28)
state <- c(X = 1, Y = 1, Z = 1)
times <- seq(0, 100, by = 1.0)
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
desolve_lorenz_solve <- function (i){
state <- c(X = runif(1), Y = runif(1), Z = runif(1))
parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}
> system.time({ lapply(1:100,desolve_lorenz_solve) })
user system elapsed
5.06 0.00 5.13
> system.time({ lapply(1:1000,desolve_lorenz_solve) })
user system elapsed
55.68 0.03 55.75
We see the expected linear scaling of a scalar code, so we can extrapolate out and see that to solve 100,000 ODEs it would take deSolve 5000 seconds, as opposed to the 14 seconds of diffeqr or the 1.8 seconds of Julia. In summary:
- Pure R diffeqr offers a 350x acceleation over deSolve
- Pure Julia DifferentialEquations.jl offers a 2777x acceleration over deSolve
Conclusion
We hope that the R community has enjoyed this release and will enjoy our future releases as well. We hope to continue building further connections to Python as well, and make the installation process as seamless as possibly by having the diffeq_setup() function automatically download and install a version of Julia if it’s not acessible from your path. Together this will make Julia a true language of libraries that can be used to accelerate scientific computation in the surrounding higher level scientific ecosystem.
The post GPU-Accelerated ODE Solving in R with Julia, the Language of Libraries appeared first on Stochastic Lifestyle.